- Conduzione termica
- Conduzione attraverso una parete piana
- Conduzione attraverso una parete piana multistrato
- Conduzione attraverso un cilindro cavo
- Conducibilità termica
- Convezione termica
- Calore sensibile: definizione e formula per il calcolo
-
Calore specifico
(tabella valori) - Calore latente per il passaggio di stato
- Calore latente e temperatura di solidificazione
- Software per progettare
- Temperatura bulbo umido e di rugiada dell'aria
-
Energia, lavoro, calore
(unità di misura) -
Calore specifico
(unità di misura) -
Coefficiente trasmissione termica
(unità di misura) -
Potenza
(unità di misura) -
Pressione
(unità di misura) -
Temperatura
(unità di misura) -
Lunghezze e distanze
(unità di misura) -
Forza e Peso
(unità di misura)
Conduzione attraverso una parete piana
Temperature e calcolo della potenza termica nel fenomeno della conduzione
Potenziale termico - Regime stazionario permanente e non permanente - Condizioni al contorno
Si consideri una parete piana, di spessore s. Ci proponamo di calcolare la quantità di calore (e quindi la potenza termica) che si trasmette per conduzione attraverso di essa a seguito della differenza di temperatura esistente tra le sue due facce opposte.
Applicando l'equazione di Fourier ed integrando tra le due superfici interna ed esterna otteniamo:
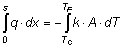
Potenza termica scambiata in regime stazionario permanente
Per calcolare la potenza termica scambiata, supponiamo che il flusso di calore avvenga in regime stazionario permanente, considerando costanti la conducibilità termica k e la superficie A possiamo scrivere:
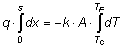
 Nell'igloo di Fred trovi anche
Nell'igloo di Fred trovi anche
Unità di misura del coefficiente di trasmissione termica e conversioni
Integrando si ottiene:
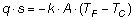
ossia:
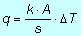
ove ΔT rappresenta la differenza tra la temperatura "calda” e la temperatura “fredda”.
 Nell'igloo di Fred trovi anche
Nell'igloo di Fred trovi anche
Risulta interessante porre la precedente equazione nella seguente forma:
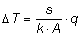
ove, posto s/kA=Rcd si ottiene
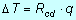
Questa equazione esprime la quantità di calore che si propaga per conduzione attraverso una parete piana in seguito alla differenza di temperatura esistente tra le sue facce: il primo membro rappresenta il potenziale termico che provoca il flusso di calore q e Rcd indica la resistenza opposta dal materiale a detto flusso di calore.
Questa equazione è formalmente analoga alla legge di Ohm valida per i circuiti elettrici in corrente continua.
Potenza termica in regime stazionario non permanente
Poichè la conducibilità termica in realtà è funzione della temperatura, l'integrazione dell'equazione di Fourier applicata ad un caso reale va eseguita in modo diverso.
Supponendo che la conducibilità dipenda linearmente dalla temperatura, allora si può scrivere:
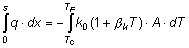
In regime stazionario è possibile procedere facilmente all'integrazione.
Dopo aver riconosciuto il prodotto notevole somma per differenza, fatte alcune semplificazioni, si giunge dopo facili passaggi alla seguente
espressione:
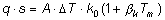
dove Tm rappresenta il valore medio (semisomma) tra la temperatura della parete calda TC e quella della temperatura fredda
TF.
Detta km la conducibilità media attraverso la parete si giunge all'espressione:
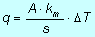
Per piccoli intervalli di temperatura, quindi, la potenza termica scambiata per conduzione dipende dalla conducibilità media km della parete che a sua volta è funzione della temperatura media dello spessore, intesa come semisomma della temperatura della superficie calda e della temperatura della superficie fredda.
Come varia la temperatura nella parete in seguito alla conduzione
Per avere un’espressione analitica dell’andamento della temperatura all’interno dello spessore s della parete è sufficiente calcolare il seguente integrale
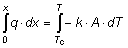
Ricordando l'equazione
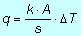
si ottiene
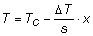
Le condizioni al contorno per l’equazione sono:
parete calda: x=0 ; T=TC
parete fredda: x=s ; T=TF
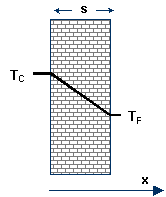
L’andamento della temperatura all’interno dello spessore s è di tipo lineare con coefficiente angolare negativo dipendente dallo spessore
della parete e dalla differenza di temperatura tra le due facce.
L'energia termica scambiata è di tipo sensibile e si esprime in joule, oppure in watt se ci riferiamo all'energia nell'unità di tempo
 Nell'igloo di Fred trovi anche
Nell'igloo di Fred trovi anche
Relazione tra energia termica, temperatura, cambiamenti di stato ed energia interna
Unità di misura dell'energia e conversioni






